|
Ahmad
7/4/2016 05:43:02 am
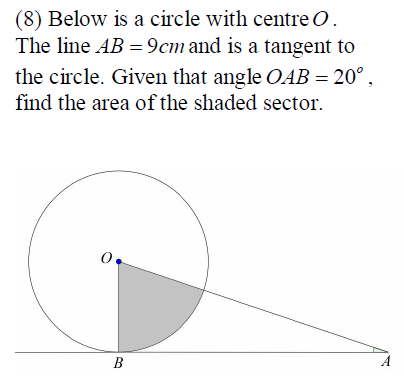
Area = 1/2 . (BO*BO)*(<BOA); <BOA is angle in radian , so,
Reply
kennedy chwala
7/4/2016 08:04:34 am
Good question , one will use sine rule to find the hypotenuse, then use pythagorus to find the adjacent= radius of the circle. Then use the formula of finding the area of the sector.
Reply
Simon Geard
22/4/2016 09:49:37 pm
Triangle AOB is right angled at B since AB is a tangent, therefore angle BOA = 70 deg ~= 1.222 rad
Reply
tom
4/5/2016 03:47:57 pm
Well, the angle at teh top left of the shaded area is 70 degrees, so that shaded area is 7/36 times the area of the circle. The radius of the circle is 9 tan(20 degrees) so its area is 81 pi times tan^2(20 degrees), which makes the area of the shaded area
Reply
Simon Geard
4/5/2016 05:35:40 pm
I think you slipped up on the last step. You should have got 63/4 (=7*81/36) - the same as Ahmad, not 28/9.
Reply
tom
5/5/2016 01:37:17 am
Ouch! 7*81/36 is right, I seem to have gone mad and chosen to use 7*36/81
tom
5/5/2016 01:40:34 am
And on top of that, I was measuring in degees instead of degrees. Must have been too much red wine at lunch.
Reply
Daniel
9/5/2016 08:45:04 am
The shaded area represents a sector so the area of a sector. To do so first we need to find the central angle which is 90 _20=79 therfore , area of a sector is (70÷360) times the area of the circle . To find the radius we will use tan 20 = r/9 then r=9tan20 ...the final answer will be (70/360)times pi times the square of 9tan 20.
Reply
Lazarus
5/10/2016 08:37:05 pm
You all lose a mark for omission of units.
Reply
Leave a Reply. |
Puzzle Ideas
If you have an idea for puzzle of the month, then please do let me know. Archives
September 2017
Don't forget to check out 'Teach Further Maths' - PowerPoints for Teachers and Students of A-Level Further Maths ...and the brilliant NEW educational card game 'Maths Trumps' |
 RSS Feed
RSS Feed


