|
Hare Ram Agarwal
2/1/2015 12:58:37 am
Radius of the circle 3.42. Perimeter of the triangle 43.84 cm or 44 cm
Reply
Paul
2/1/2015 02:16:39 am
Thanks Hare Ram. Would you care to elaborate?
Reply
Hare Ram Agarwal
2/1/2015 03:49:51 am
Taking radius as r and hypotenuse as 12.5 + x,
Reply
2/1/2015 03:01:38 am
I agree with 43.84 (44) cm with radius 3.42 to 2 dp
Reply
Paul
2/1/2015 06:08:53 am
Thanks to Hare Ram and John. Let's see what others some up with. John, your notation is fine but I know what you mean.
Reply
Andrey Dyukmedzhiev
2/1/2015 12:10:29 pm
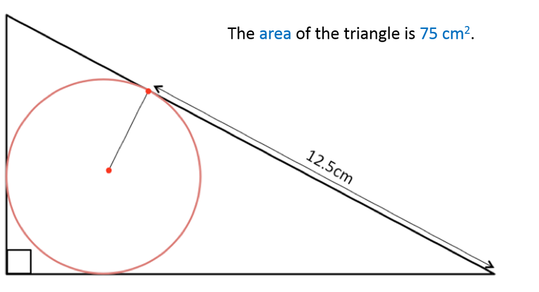
Here is a general approach, using Heron's formula. Let A is the area, s - semi-perimeter; a, b - legs (a - vertical, b - horizontal on the diagram above), c - hypotenuse, r - inradius. For every triangle the segments, connecting vertices with touching points with the inscribed circle have lengths
Reply
Williamson
4/1/2015 11:33:35 am
Andrey, I tried to use the Heron formula and I realized I was not going anywhere. But you kept going. which was good. Either way I was supposed to keep it going and I would have gotten a simplest equation. But nice steps as always
Reply
2/1/2015 05:46:55 pm
I recognized this as a non-linear intersection problem. I crunched it down to a 1 variable equation, by using the constraint on the triangle area: 150 = (12.5 + r) * (r + b )
Reply
3/1/2015 12:24:25 am
Interesting discussion. My first thoughts were to use Heron's and incircle facts, leading to the solution discussed here:http://wp.me/p2z9Lp-on
Reply
Williamson
4/1/2015 11:29:55 am
I tried to use the Heron formula too, but I did not go anywhere. So I refocus on the fact that the 3 sides in the triangle were tangent to the circle. That is what gave me a few break. However, the equation that I found to solve for the radius became a 3rd degree polynomial and I did not want to solve it. :)
Reply
Paul
3/1/2015 01:29:02 am
Thanks to Andrey and Pierre for your impressive contributions. And Stephen, many thanks for bringing this problem to my attention. It was always going to bring out a great discussion. I'm sure there will be more to come out of this.
Reply
Williamson
4/1/2015 11:25:53 am
I do not see where I made my mistake, but I do not see the perimeter is 43.84. Assume the side of the triangles are named A, B, C where A is the shortest side, B is the medium side, and C is the longest side (Hypotenuse). We have a triangle with area 75 cm^2 and a circle with radius R. Since the hypotenuse of the triangle is tangent to the circle; therefore, the radius of the circle is perpendicular to the hypotenuse. The side of the hypotenuse is x + 12.5. Draw another radius from the center of the circle connect to side B which is tangent to the circle again. Hence The side B is perpendicular to the 2nd radius of the circle. A third radius will be perpendicular to the side A as well. Since the 2nd radius is perpendicular to the side B, hence it will for a square with sides R. Because of the tangents the sides are to the circle, A = x + R, B = 12.5 + R and C = 12.5 + x. The area of the triangle is 1/2 Base x Height. B is the base and A is the height. Hence 1/2 (12.5+R)(x+R) = 75. Hence (12.5+R)(x+R) = 150. Solve for x, we have x = 150/(12.5+R) - R EQ(1). Connect two lines from each non right angle vertex to the center. We will have 4 triangles and one square with sides R. In the 4 triangles, 2 of them are congruent with base R and height x and the other 2 triangles are congruent with base 12.5cm and Height R.
Reply
Leave a Reply. |
Puzzle Ideas
If you have an idea for puzzle of the month, then please do let me know. Archives
September 2017
Don't forget to check out 'Teach Further Maths' - PowerPoints for Teachers and Students of A-Level Further Maths ...and the brilliant NEW educational card game 'Maths Trumps' |
 RSS Feed
RSS Feed


