|
This puzzle is kindly provided by UKMT. A point is chosen at random inside a square QRST.
20 Comments
Ms
2/3/2014 10:45:03 pm
3/4 would be my first guess
Reply
Mehtamatics
4/3/2014 05:52:28 am
Anywhere outside the semicircle on QR. So I go for 1-pi/8
Reply
5/4/2014 07:47:29 pm
Your answer is correct but you omitted the proof. See my proof in my separate comment below.
Reply
4/3/2014 12:16:09 pm
The diagonals of the square cut it into quarters. Only when P is in the left hand quarter will the angle be obtuse. Therefore probability of an acute angle is 3/4.
Reply
Adel A. Abdelkarim
7/3/2014 01:30:30 am
The probability is (8-pi)/8. For it is the ratio of the difference between the square area and a half circle with diameter being the left side of the square to the area of the square.
Reply
Brian
8/3/2014 06:32:20 pm
OK, so some say 75% and others say 60.7%. I understand both sets of logic and side with the 61%.
Reply
Tom
14/3/2014 07:56:14 pm
I agree with Brian - 1-π/8 is clearly right. I can't understand the 75% answer, even ignoring the angle in a semicirle, because it's obvious that if P lies on a diagonal and is very close to Q or to R the angle QPR is very close to 135 degrees, and since small movements of P cause small changes in the angle (the angle is given by a continuous function of teh position of P) moving P a small distance outside the LH quarter from such a point will leave the angle not much smaller that 135 degrees, so more than the left hand quarter delivers more than 90 degrees and less than 75% delivers an acute angle.
Reply
Charles greene
14/3/2014 09:30:06 pm
Ok i am going low on this i was seeing 50% is this just a tired mind missing the obvious. Rigth side acute left side obtuse?
Reply
David Esparza
15/3/2014 01:28:18 am
Use law of cosines. Call side
Reply
David Esparza
15/3/2014 01:47:36 am
There is another way of doing the calculation, this time by approximation by Monte Carlo.
Reply
Paul
15/3/2014 02:34:35 am
Thanks everyone. I'm loving the discussion and the alternative methods of solving this.
Reply
Tom
15/3/2014 05:05:00 am
A more elementary approach than the method of cosines is simple repetition of Pythagoras' rule for right triangles. If we take the length of the perpendicular from P to QT as x and that of the perpendicular from P to QR as y, and assume that the angle QPR is <= pi/2, we have PR >1, and by applying Pythagoras law to teh two right triangles pQT and PQR that is x^2+y^2+x^2+(1-y)^2>=1, simplifying this we have 2x^2+(y-1)^2+y^2>=1, hence x^2+y^2-y+0.5>0.5, or
Reply
tom
15/3/2014 05:08:42 am
Ouch, at the end of my last comment for "midpoint of QR" read "midpoint of QT". silly mistake. Makes no difference to the number, though.
Reply
Hare Ram Agarwal
27/3/2014 01:57:44 am
Area of the region where the angle will not be acute = semicircle with QR as diameter = 0.5 x pi x (QR/2)^2
Reply
29/3/2014 12:50:28 pm
Here is a vector-based proof for the angle inscribed in a semicircle.
Reply
Paul
30/3/2014 03:02:16 am
Thanks to Hare Ram and Pierre for more excellent contributions. I hope next month's puzzle is as successful as this one has been.
Reply
Gerry Rising
4/4/2014 01:31:06 pm
Older sailors familiar with danger angle navigation will appreciate this problem. Points on the semicircle on side RQ make angle RPQ a right angle. Thus angles RPQ with P inside that semicircle are obtuse; angles outside acute. The proofs are nice geometry exercises.
Reply
5/4/2014 07:44:39 pm
The probability is 1-(pi/8)=0.6073. Proof: (1) A triangle inscribed in a semicircle (with the diameter as a base) is a right triangle. (2) If the point is inside the semicircle then it forms an angle greater than 90 degrees. If the point is outside the semicircle it forms an acute angle. Assume without loss of generality that the sides of the square are equal to one; so the radius of the inscribed semicircle is 1/2 and its area equals pi/8. Consequently the area outside the semicircle is 1-(pi/8). QED
Reply
karen
7/4/2014 09:06:24 am
0 (acute angles are < 90 and all angles in a square are 90)
Reply
Leave a Reply. |
Puzzle Ideas
If you have an idea for puzzle of the month, then please do let me know. Archives
September 2017
Don't forget to check out 'Teach Further Maths' - PowerPoints for Teachers and Students of A-Level Further Maths ...and the brilliant NEW educational card game 'Maths Trumps' |
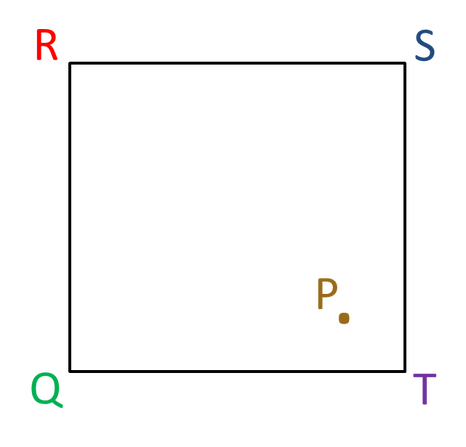


 RSS Feed
RSS Feed


