|
Andrey Dyukmedzhiev
7/11/2014 02:28:53 am
The computer search immediately found 1 + 2 + 4 + 66 = 73. Since the searching code was 2-3 lines long and took me less than a minute, I haven't yet looked deeper into the puzzle.
Reply
Paul
7/11/2014 09:23:17 am
Thanks Andrey. I'll look forward to more of your thoughts on this.
Reply
Simon
7/11/2014 10:17:38 am
Yes I also did a computer search and found the answer to be 73, with a,b,c,d being any permutation of 1,2,4,66. Code below for anyone interested.
Reply
Jim Walker
7/11/2014 10:42:09 am
They are the coefficients of a polynomial of degree 4. If you rewrite the equation as (x+a)(x+b)(x+c)(x+d)=2009 + x^4 and let x = 1, the equation becomes (1+a)(1+b)(1+c)(1+d) = 2010. Factor 2010 and you find the answers.
Reply
Simon
7/11/2014 10:47:49 am
I'm not suprised, it certainly looked as if it were susceptible to factorization. I had got as far as working out that they couldn't all be the same since (a+1)**4 = 2010 has no integer solutions - I even looked up the prime factors of 2010 but didn't make the final connection. On the other hand I like writing softwae so that's what I did.
Reply
7/11/2014 11:26:30 am
A used a search algorithm in Java, constrained by the largest value for a being 2009/8, since the b,c,d values are at least 1.
Reply
7/11/2014 03:17:52 pm
(1+a)*(1+b)*(1+c)*(1+d) = your expression + 1
Reply
Andrey Dyukmedzhiev
7/11/2014 10:33:33 pm
Yes, the same thing came to my mind, but it was too late. Knowing that a computer search will do the job make someone's mind lazy. Congratulations for the nice solution!
Reply
Williamson
8/11/2014 09:07:35 pm
Your step was easier :)
Reply
Williamson
8/11/2014 09:02:00 pm
I did fine the same answer too, but I did it in a different approach. Here is the step that I did. I combine both the abcd and abc together and factorize abc. That is; abc(d+1) . Then I factorize all the other terms until I get (d+1) as a common factor for all the terms left. I will have only left the letter d as term alone. Then inside of the factorization, I keep factoring so that I can have a variable + 1. In that case, base on the factorization, I assume d has its last digit 1. But I know 1 + 8 = 9 which is the last digit of 2009. The term that will be added to d will need to have its last digit 8 so that 8 + 1 = 9. Then from that factorization, I proceed with the possibility of the other letters to find out what could be their last digit. Here is how I did it below:
Reply
Paul
8/11/2014 11:17:29 pm
Many thanks to the contributors of these comments. I thoroughly enjoy reading your thoughts, comments and great solution techniques. Let's see if anyone else finds a different approach...
Reply
11/11/2014 10:34:35 am
Paul , it seems that I could have done it a simpler way. With the solutions given with the other people. after my first factorization, I could have add 1 to both sides to make the other term become 2010. From there I could of work my factorization by grouping. I believe I could have had the answer that way too.
Reply
Paul
11/11/2014 11:22:29 pm
Great stuff, Williamson.
Reply
Brent
17/11/2014 08:32:26 am
I tried some simple examples to see if I could solve for d, first setting a=b=c=1, then a=b=1 and c=2, and two or three more cases. I noticed that in each case it added up to
Reply
Paul
17/11/2014 09:46:23 pm
And thanks for your enthusiastic and well-thought out response, Brent.
Reply
TomThomson
23/11/2014 02:53:00 pm
Interesting.
Reply
Leave a Reply. |
Puzzle Ideas
If you have an idea for puzzle of the month, then please do let me know. Archives
September 2017
Don't forget to check out 'Teach Further Maths' - PowerPoints for Teachers and Students of A-Level Further Maths ...and the brilliant NEW educational card game 'Maths Trumps' |
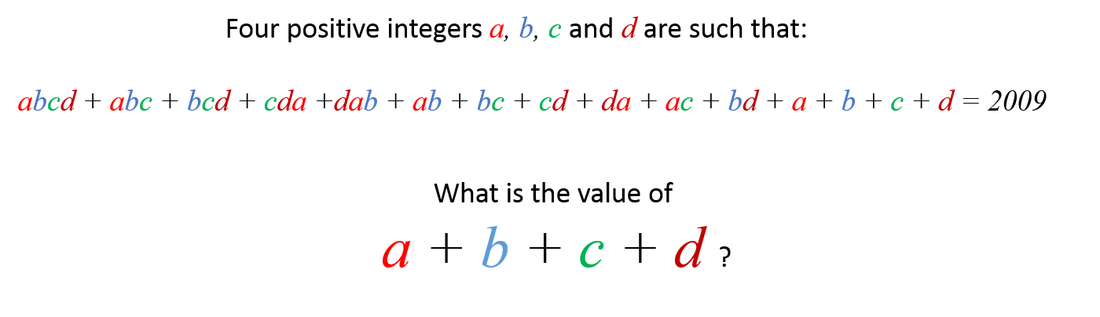
 RSS Feed
RSS Feed


