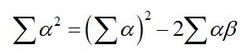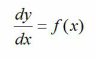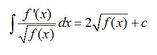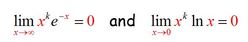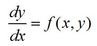Superb PowerPoint Teaching Resources for Teachers of A-Level Further Maths

"...student friendly and should be in every school in the UK!"
​
​

A selection of some of the most outstanding and inspiring mathematicians in history.

​What is 'Teach Further Maths'?

Written for teachers, 'Teach Further Maths' is a suite of high quality, fully animated colour A-Level Further Maths PowerPoint presentations, consisting of over 3000 slides.
 
Written by a very experienced classroom practitioner, examiner and published maths author (Paul Hunt), the presentations include demonstrations, proofs, worked examples, exercises, exam-style questions and actual exam questions (used with permission). 
 
'Teach Further Maths' is perfect for the new specifications and already includes most of the compulsory content from all of the main examination boards.
​

Which topics does 'Teach Further Maths' cover?

Teach Further Maths now includes full, detailed coverage of EVERY topic from the compulsory content that teachers now have to deliver.

All 4 of the main exam boards are now completely catered for!

(see the table below for details of the compulsory A-Level Further Mathematics content for each of Edexcel, AQA, OCR and MEI).

​Screenshots from 'Teach Further Maths':

A small sample of what to expect from 'Teach Further Maths':

DeMoivre's Theorem & Applications 2 © P. A. Hunt 2017

Improper Integrals © P. A. Hunt 2017

2nd Order Differential Equations © P. A. Hunt 2017

Matrix Solution of Simultaneous Equations 2 © P. A. Hunt 2017

​Can I try before I buy?

Not as such, but we do offer a completely free Sample presentation (from the A-Level Mathematics specification) so that you can experience the high quality of presentations that 'Teach Further Maths' offers you.
​
​

Compulsory A-Level Further Mathematics content by exam board

Topic	Content	Edexcel	AQA	OCR 'A'	MEI
Proof	Construct proofs by mathematical induction	Included	Included	Included	Included
Complex Numbers	Solve any quadratic with real coefficients	​Included	Included	Included	Included
Complex Numbers	Solve cubic or quartic equations with real coefficients	Included	​Included	Included	Included
Complex Numbers	Add, subtract, multiply and divide complex numbers; understand the terms 'real' part and 'imaginary' part, 'modulus' and 'argument'	Included	​Included	​Included	​Included
Complex Numbers	Understand and use the complex conjugate; know that non-real roots of polynomials equations with real coefficients occur in conjugate pairs	Included	Included	Included	​​​Included
​Complex Numbers	Use and interpret Argand diagrams	Included	Included	Included	​​Included
Complex Numbers	Convert between Cartesian form and Modulus-Argument form of a complex number	​Included	​Included	​​​Included	​​Included
Complex Numbers	Multiply and divide complex numbers in modulus-argument form	​Included	Included	​​Included	​​Included
​Complex Numbers	Construct and interpret simple loci in an Argand diagram.	Included	Included	​​Included	​​​Included
​Complex Numbers	Know and use both forms of Euler's formula (*)	​Included​	​​Included	​​Included	​​​Included
Complex Numbers	Understand and use DeMoivre's Theorem and use it to find the multiple angle formulae and sums of series	​​Included	​Included	​​Included	​​Included
​Complex Numbers	Find the nth roots of any complex number and know that they form the vertices of a regular n-sided polygon in the Argand diagram	​​Included	​​Included	​​​Included	​​​Included
Complex Numbers	Use complex roots of unity to solve geometric problems	​​Included	​​​Included	​​Included	​​Included
Matrices	Add, subtract and multiply conformable matrices; multiply a matrix by a scalar	​Included	Included	​​​Included	​​Included
Matrices	Understand and use zero and identity matrices	Included	​Included	​​Included	​​​Included
Matrices	Know that matrix multiplication is associative but not commutative	Included	Included	​​​Included	​​Included
Matrices	Find and use matrices to represent linear transformations in 2D (including simple shears)​; successive transformations; 3D transformations confined to simple cases only	Included	​Included	​​​Included	​​Included
Matrices	Find invariant points and lines for a linear transformation​	​Included	​Included	​​​Included	​​Included
Matrices	Find the determinant of 2 x 2 and 3 x 3 matrices.	Included	Included	​​​Included	​​Included
Matrices	Know that the determinant of a 2 x 2 matrix is the area scale factor of the associated transformation  and interpret the sign of the determinant in terms of the orientation of the image.	​​​Included	​​Included	​​Included	​​​Included
Matrices	Calculate the inverse of 2 x 2 and 3 x 3 non-singular matrices	​Included	​Included	​​​Included	​​Included
Matrices	Solve 3 simultaneous linear equations in 2 variables by use of the inverse matrix	Included	Included	​​Included	​​​Included
Matrices	Interpret geometrically the solution and failure of solution of 3 simultaneous equations	​​​Included	​​​Included	​​Included	​​​Included
Matrices	​Factorisation of determinants using row and column operations	N/A	​​Included	N/A	N/A
Matrices	Find the eigenvalues and eigenvectors of 2 x 2 and 3 x 3 matrices; find and use the characteristic equation	N/A	Included	​N/A	​N/A
​Matrices	Diagonalise matrices	​N/A	​Included	​N/A	​N/A
Further Algebra	Understand and use the relationship between roots and coefficients of polynomial equations up to quartic equations.	Included	Included	​​​Included	​​​Included
Further Algebra	Form a polynomial equation whose roots are a linear transformation of the roots of a given polynomial	Included	Included	​​​Included	​​​Included
Further Algebra	Understand and use formulae for sums of integers, squares and cubes and use these to sum other series	Included	​Included	​​​Included	​​​Included
Further Algebra	Understand and use the method of differences for summation of series including use of partial fractions	Included	Included	​​​Included	​​​Included
Further Algebra	Find the MacLaurin series of a function, including its general term	Included	​Included	​​Included	​​Included
​Further Algebra	Recognise and use Maclaurin series for certain functions and be aware of their range of validity	Included	Included	​​​Included	​​Included
Further Algebra	Evaluation of limits using MacLaurin series (L'Hopital's Rule also included)	Included	​Included	​​​Included	​​Included
Further Algebra	Inequalities involving polynomial equations (cubic and quartic)	N/A	​​Included	​N/A	N/A
Further Algebra	Solving rational inequalities algebraically (**)	​N/A	Included	N/A	​N/A
Further Algebra	Modulus of functions and associated inequalities	N/A	​​​Included	N/A	​N/A
Further Algebra	​Graphs of rational functions with linear numerator/denominator; asymptotes, points of intersection	N/A	Included	​N/A	​N/A
Further Algebra	Graphs of rational functions with quadratic numerator/denominator	N/A	Included	N/A	N/A
Further Algebra	Quadratic theory (not calculus) for rational functions with quadratic numerator/denominator; stationary points	N/A	Included	N/A	​N/A
Further Algebra	Sketching curves of parabolas, ellipses and hyperbolas (***)	N/A	Included	N/A	N/A
Further Algebra	Single transformations of curves involving translations, stretches parallel to the coordinate axes and reflections in the lines y = x and y = -x; Extend to composite transformations including rotations and enlargements	N/A	Included​	​N/A	​N/A
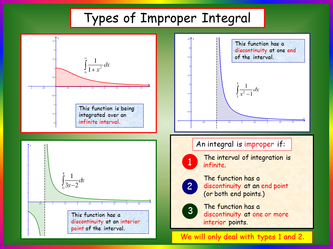
Further Calculus	Evaluate improper integrals where either the integrand is undefined at a value in the interval of integration or the interval of integration extends to infinity	​Included	​Included	​​​Included	​​Included
Further Calculus	Derive formulae for and evaluate volumes of revolution	​​Included	​​Included	​​​Included	​​Included
​Further Calculus	Understand and evaluate the mean value of a function	​​Included	​​Included	​​​Included	​​​Included
Further Calculus	Integrate using partial fractions (extend to quadratic factors in the denominator)	​​Included	​​Included	​​​Included	​​​Included
Further Calculus	Differentiate inverse trigonometric functions	Included	Included	​​​Included	​​​Included
Further Calculus	Integrate functions of the form (****) and choose appropriate trigonometric substitutions to integrate associated functions	Included	Included	​​​Included	​​​Included
Further Calculus	Arc length and surface of area of revolution for curves expressed in Cartesian or parametric form	N/A	Included	N/A	​N/A
Further Calculus	Derivation of use of reduction formulae for integration	N/A	​​​Included	​N/A	N/A
Further Calculus	Know and use two special limits (*****) applied to improper integrals	N/A	Included	N/A	N/A
Further Vectors	Understand and use the vector and Cartesian form of an equation of a straight line in 3D	Included	Included	​​​Included	​​Included
Further Vectors	Understand and use the vector and Cartesian forms of an equation of a plane.	Included	Included	​​​Included	​​Included
​Further Vectors	Calculate the scalar product and use it to express the equation of a plane, and to calculate the angle between two lines, the angle between two planes and the angle between a line and a plane.	Included	Included	​​​Included	​​Included
Further Vectors	Find the intersection of a line and line; Find the intersection of a line and a plane; Calculate the distance from a point to a line and from a point to a plane.	Included	Included	​​​Included	​​Included
Further Vectors	Be able to determine whether two lines in 3 dimensions are parallel, skew or intersect, and find the point of intersection if there is one.	Included	​Included	​​​Included	​​​Included
Further Vectors	Be able to find the distance between two parallel lines and the shortest distance between two skew lines	​​​Included	​​​Included	​​Included	​​​Included
Further Vectors	Be able to use the vector product to find a vector perpendicular to two given vectors	​​Included	​​Included	​​​Included	​​Included
Further Vectors	Understand and use the equation of a straight line in the form (r - a) x b = 0; use vector products to find the area of a triangle	​​Included	​​​Included	​​​Included	​​​Included
Polar Coordinates	Understand and use polar coordinates, and be able to convert between polar and Cartesian coordinates	Included	​Included	​​​Included	​​Included
​Polar Coordinates	Sketch curves with simple polar equations where r is given as a function of theta	​Included	​Included	​​​Included	Included
Polar Coordinates	Be able to find the area enclosed by a polar curve	Included	Included	​​​Included	​​Included
Hyperbolic Functions	Understand and use the definitions of hyperbolic functions, including their domains and ranges, and be able to sketch their graphs	Included	Included	​​Included	​​​Included
Hyperbolic Functions	Understand and use the definitions of inverse hyperbolic functions and their domains and ranges.	Included	Included	​​​Included	​​​Included
Hyperbolic Functions	Differentiate and integrate hyperbolic functions	Included	Included	​​​Included	​​​Included
​Hyperbolic Functions	Derive and use logarithmic forms of the inverse hyperbolic functions.	Included	Included	​​​Included	​​​Included
Hyperbolic Functions	Integrate functions of the form (******) and choose appropriate hyperbolic substitutions to integrate associated functions	​Included	Included	​​​Included	​​​Included
Hyperbolic Functions	Construct proofs involving hyperbolic functions and identities	​Included	Included	​​​Included	​​Included
Differential Equations	Find and use the integrating factor to solve differential equations of the form y'(x) +P(x)y=Q(x) and recognise when it is appropriate to do so	​Included	​Included	​​​Included	​​Included
​Differential Equations	Find both general and particular solutions to differential equations	​Included	​Included	​​​Included	​​Included
Differential Equations	Use differential equations in modelling in kinematics and in other contexts	​​Included	​​Included	​​​Included	​​​Included
Differential Equations	Solve differential equations of the form y'' +ay' +by =0, where a and b are constants, by using the auxiliary equation	​Included	​Included	​​​Included	​​​Included
Differential Equations	Solve differential equations of the form  y'' +ay' +by = f(x), where a and b are constants, by solving the homogeneous case and adding a particular integral to the complementary function.	​​Included	​Included	​​​Included	​​​Included
Differential Equations	Understand and use the relationship between cases when the discriminant of the auxiliary equation is positive, negative and zero, and the form of solution of the differential equation	​Included	​Included	​​​Included	​​Included
Differential Equations	Solve the equation for simple harmonic motion and relate the solution to motion	​​Included	​​Included	​​​Included	​​Included
Differential Equation	Model damped oscillations using second order differential equations and interpret their solutions	​​Included	​​Included	​​Included	​​​Included
Differential Equations	Analyse and interpret models of situations with one independent variable and two dependent variables as a pair of coupled first order simultaneous equations and be able to solve them, for example predator-prey models	​​Included	​​Included	​​​Included	​​Included
Numerical Methods	Mid-ordinate rule and Simpson's rule for integration	N/A	​​Included	​N/A	N/A
​Numerical Methods	Euler's step-by-step method and The Mid-Point Method for solving 1st order differential equation	N/A	Included	​N/A	​N/A
​Numerical Methods	Improved Euler Method for solving 1st order differential equations	N/A	Included	N/A	N/A

​
​A-Level Further Mathematics

PowerPoint Presentations containing Compulsory Teaching content

(Please that the number of slides stated is an approximate guide only.)

F1. Asymptotes and Rational Functions

·         To understand what is meant by an ‘asymptote’.

·         To know how to find the equations of horizontal asymptotes.

·         To know how to find the equations of vertical asymptotes.

·         To be able to sketch the graphs of some rational functions.

(32 Slides)

F2. Complex Numbers 1​
(Formerly F3)

·         To understand what is meant by an ‘imaginary number’.

·         To be able to calculate with powers of i.

·         To understand what is meant by a ‘complex number’.

·         To be able to solve any quadratic equation.

·         To know the condition for a quadratic equation to have complex conjugate solutions.

·         To understand what is meant by an ‘Argand Diagram’.

·         To be able to perform simple arithmetic with complex numbers.

(37 Slides)

F3. First Order Differential Equations​
(Formerly F4)

·       To understand what is meant by a ‘linear, first order differential equation’.

·         To recall how to solve some linear first order differential equations by separating variables.

·         To know what is meant by a ‘Family of Solution Curves’.

·         To know how to solve some linear first order differential equations using an integrating factor.

(37 Slides)
​

---

F4. Improper Integrals 1​
(Formerly F5)

·         To understand what is meant by an ‘improper integral’.

·         To be able to evaluate simple improper integrals.

(12 Slides)

F5. Matrices​
(Formerly F7)

·         To understand simple matrix terminology - e.g. ‘matrix’, ‘order’.

·         To be able add, subtract and multiply compatible matrices.

·         To be able to ascertain whether or not matrix multiplication is commutative/associative.

·         To know and use the properties of ‘square’, ‘identity’ and ‘zero’ matrices.

(64 Slides)
​

F6. Inequalities Involving Rational Expressions​
(Formerly F8)

·        To recall how to solve simple inequalities.

·         To be able to solve inequalities involving rational expressions.

(41 Slides)
​

---

F7. Polar Coordinates 1
(Formerly F9)​

·         To understand what is meant by ‘Polar Coordinates’.

·         To be able to plot Polar Coordinates.

·         To be able to sketch curves given in Polar form.

·         To understand that some simple polar curves can be sketched without plotting points.

(42 Slides)

F8. Roots of Quadratics​
(Formerly F10)

·          To understand and use the relationship between the roots and coefficients of a quadratic equation.

·         To find quadratic equations with related roots.

(61 Slides)

F9. Matrix Transformations​
​(Formerly F12)

To be able to use algebra to solve simple transformations problems.

·         To be able to find matrices associated with common matrix transformations.

·         To be able to describe transformations represented by certain matrices.

(64 Slides)
​

---

F10. More Asymptotes and Rational Functions​
(Formerly F13)

·        To be able to sketch curves for certain rational functions.

·         Find the regions for which certain rational functions actually exist.

·         Find stationary points without the use of calculus.

(46 Slides)
​

F11. Polar Coordinates 2
(Formerly F14)​

·         To be able to convert Polar form to Cartesian form.

·         To be able to convert Cartesian form to Polar form.

·         To use integration to find areas bound by Polar curves.

·         To be able to find equations of tangents at the pole.

·         To be able to find equations of tangents parallel (or perpendicular) to the initial line.

(73 Slides)

F12. Second Order Differential Equations​
(Formerly F15)

·         To understand what is meant by a ‘second order differential equation’.

·         To be able to solve some second order differential equations using the auxiliary equation.

·         To be able to solve some second order differential equations by finding a complementary function and a particular integral.

(78 Slides)

---

F13. Complex Numbers 2​
(Formerly F16)

·         To understand what is meant by an Argand Diagram.

·         To understand what is meant by the Modulus and Argument of a complex number.

·         To be able to divide one complex number by another complex number.

·         To solve equations using Real and Imaginary parts.

·         To understand what is meant by Modulus-Argument form.

·         To multiply and divide complex numbers written in modulus-argument form.

(55 Slides)

F14. Improper Integrals 2​
(Formerly F18)

·     To know what is meant by an ‘improper integral’.

·         To know how to find further improper integrals.

(23 Slides)

F15. Roots of Polynomials​
(Formerly F19)

·          To know the relationship between the roots of a polynomial equation and its coefficients.

·         To be able to find polynomial equations with related roots.

·         To know and use the result

(65 Slides)

---

F16. Graphical Solution of Inequalities​
(Formerly F20)

·         To be able to inequalities involving rational expressions using a graphical method.

(34 Slides)
​

F17. Composite Geometric Transformations Using Matrices
(Formerly F21)​

·        To recall the rules of simple transformations.

·         To be able to find matrices representing simple composite transformations.

·         To know that composite transformation matrices are pre-multiplied.

·         To be able to describe simple composite transformations represented by some matrices.

(28 Slides)

F18. Numerical Methods​
(Formerly F23)

·         To be able to solve equations of the form f(x) =0 using the method of interval bisection.

·         To be able to solve equations of the form f(x) =0 using the method of linear interpolation.

·         To be able to solve equations of the form f(x) =0 using the Newton-Raphson method.

·         To be able to solve equations of the form

using Euler's 'step by step' method.

(59 slides)

---

F19. Hyperbolic Functions​
(Formerly F24)

To understand what is meant by hyperbolic functions.

·         To be able to sketch graphs of hyperbolic functions.

·         To be able to establish hyperbolic identities.

·         To understand Osborn’s Rule.

(31 Slides)

F20. Inverse Trigonometric Functions​
(Formerly F25)

​F21. More 1st and 2nd Order Differential Equations 1
(Formerly F26)

·            To sketch graphs of inverse trigonometric functions.
·         To be able to differentiate inverse trigonometric functions.

·         To recognise integrals which integrate to inverse trigonometric functions.

·         To integrate more complicated expressions

·         To know the result

(47 Slides)

·         To be able to solve certain first order differential equations using a complementary function and a particular integral.

·         To use a change of variable to solve some first and second order differential equations.

(30 Slides)

---

F22. Polar Coordinates 3​

·        To use the skills learnt so far to solve exam style polar geometry questions.
(Formerly F27)

(20 Slides)
​

F23. Complex Roots of Polynomials with Real Coefficients​
(Formerly F28)

·      To understand that, for a polynomial with real coefficients, any complex roots occur in conjugate pairs.

·         To use this condition in solving various problems about complex roots of polynomials.

(33 Slides)
​

F24. Series​
(Formerly F29)

To understand and use Sigma notation.

·         To be able to derive and use the formula for ∑r.

·         To be able to use the formulae for

.        To be able to solve series questions requiring algebraic manipulation.

(47 Slides)

---

F25. Matrices and Linear Transformations
(Formerly  F30)​

·         To understand what is meant by a ‘transformation’ and by a 'linear transformation'

·         To be able to show that a given transformation is linear.

·         To understand what is meant by an ‘inverse transformation’.

·         To be able to find the inverse of a given linear transformation.

·         To be able to find matrices that represent given linear transformations.

·         To be able to find matrices that represent composite linear transformations.

·         To understand what is meant by ‘invariant points’ and ‘invariant lines’.

·         To be able to find invariant points/lines for a given transformation matrix.

·         To be able to find matrices representing inverse linear transformations.

·         To be able to find matrices representing inverse of composite linear transformations.

·         To understand how to find the transpose of a matrix.


(73 Slides)

F26. De Moivre's Theorem and Applications 1​
(Formerly F31)

·         To recall how to multiply and divide complex numbers in Modulus-Argument form.

·         To understand DeMoivre’s Theorem.

·         To use DeMoivre’s Theorem to find powers of complex numbers.

·         To use DeMoivre’s Theorem to establish trigonometric identities.

(43 Slides)
​

F27. Differentiation of Hyperbolic Functions​
(Formerly F32)

·         To be able to differentiate hyperbolic functions.

·         To be able to sketch graphs of hyperbolic functions.

·         To be able to differentiate inverse hyperbolic functions.

·         To be able to sketch graphs of inverse hyperbolic functions.

·         To write inverse hyperbolic functions in logarithmic form.

(36 Slides)

---

F28. Exponential Form of a Complex Number​
(Formerly F33)

·         To write a complex number in exponential form.

·         To multiply and divide complex numbers in exponential form.

(18 Slides)

F29. Inverse Matrices and Determinants​
(Formerly F35)

·        To understand what is meant by the ‘inverse’ of a matrix.

·         To understand what is meant by the ‘determinant’ of a matrix.

·         To be able to find the determinant of a 2x2 or 3x3 matrix.

·         To be able to find the inverse of a 2x2 or 3x3 matrix.

·         To be able to consider determinants of 2x2 matrices and 3x3 matrices geometrically.


(54 Slides)​

F30. Matrix Solution of Simultaneous Equations 1
(Formerly F36)

  To be able to solve linear simultaneous equations by finding the inverse of a matrix.

·         To appreciate that the determinant can be used to determine the existence (or not) of a unique solution for a system of linear simultaneous equations.


(28 Slides)​

---

F31. MacLaurin's Series
(Formerly F37)

·         To be able to use MacLaurin’s Series to find series expansions.

·         To be able to find the Ranges of Validity for certain series.

(38 Slides)

F32. Parabolas, Ellipses and Hyperbolas
(Formerly F38)

​·         To be able to recognise the equations for simple parabolas, ellipses and hyperbolas.

·         To be able to sketch their graphs.

·         To be able to perform simple transformations on these curves.

·         To be able to find the equations of the asymptotes for simple hyperbolas.

(70 Slides)

F33. The Method of Differences
(Formerly F39)

·         ​To understand the Method of Differences.

·         To be able to use the Method of Differences to prove results for the summation of certain series.

(17 Slides)

---

F34. Loci in the Complex Plane
(Formerly F40)

·         To be able to sketch loci on an Argand Diagram.

(52 Slides)

F35. De Moivre's Theorem and Applications 2​
(Formerly F42)

To find the cube roots of unity.

·         To illustrate these cube roots on an Argand Diagram.

·         To solve problems relating to the cube roots of unity.

·         To find the nth roots of unity.

·         To illustrate these nth roots on an Argand Diagram.

·         To find the nth roots of any number.

(57 Slides)

F36. Integration with Hyperbolic Functions​
(Formerly F43)

To recall the derivatives of hyperbolic functions.

·         To be able to integrate hyperbolic functions.

·         To recognise integrals which integrate to inverse hyperbolic functions.

(35 Slides)
​

---

F37. Limits of MacLaurin's Series
(Formerly F44)​

 To recall the concept of a ‘limit’.

·         To be able to use MacLaurin’s series expansions to find certain limits.

·         To know and use the special limits

(45 Slides)

F38. More 1st and 2nd Order Differential Equations 2​
(Formerly F45)

·        To understand the chain rule when using first and second order derivatives.

·         Use a substitution in conjunction with the chain rule to solve certain second order differential equations.

(38 Slides)

F39. Numerical Methods for 1st Order Differential Equations​
(Formerly F46)

·         To be able to solve first order differential equations of the form​

 using the following 'step by step' methods
​

• Euler's Method
• The Mid-Point Method
• The Improved Euler Method

(58 slides)

---

F40. Proof by Mathematical Induction​
(Formerly F47)

·          To understand the method of Mathematical Induction.

·         To use Induction to prove results for summation of series.

·         To use Induction to prove results from other areas.

(49 Slides)

F41. Solving Hyperbolic Equations
(Formerly F48)​

 To be able to solve hyperbolic equations.

(13 Slides)
​

F42. Eigenvalues and Eigenvectors
(Formerly F49)

 To understand what is meant by ‘eigenvalues’ and ‘eigenvectors’.

·         To understand how to find the ‘characteristic equation’.

·         To be able to find eigenvalues and eigenvectors for given 2x2 and 3x3 matrices.

·         Understand what is meant by the terms ‘normalised eigenvectors’, ‘orthogonal eigenvectors’ and ‘orthogonal matrices’.

·         To be able to show that a given matrix is orthogonal. 


(54 Slides)​

---

F43. Diagonalisation of a Matrix​
(Formerly F50)

·         To understand what is meant by ‘diagonal matrices’ and ‘symmetric matrices’.

·         To understand what is meant by ‘diagonalising’ a matrix.

·         To be able to deduce diagonalisability for simple 2x2 and 3x3 matrices.

·         To be able to diagonalise a given symmetric matrix.

·         To apply the method of diagonalisation to evaluate the power of a given symmetric matrix.


(40 Slides)​

F44. Further Vectors 1
​NEW

• To be able to find the distance between 2 points in 3 dimensions.

​

• To be able to derive and use a useful formula for a point dividing a line in a given ratio.​

• To understand when 2 (or more) vectors are parallel.

​

• To be able to find vector equation of a line in vector form.

​​

• To be able to find vector equation of a line in Cartesian form.

​

• To be able to convert vector equations from vector form to Cartesian form and vice versa.

​​

• To understand what direction ratios are

(43 Slides)​

F45. Further Vectors 2
​NEW

• To understand the ‘scalar product’ and be able to calculate it.​

​

• To be able to find the angle between two vectors using the scalar product​

• To use the scalar product to show whether two lines are perpendicular or not.​

• To be able to prove whether or not two lines intersect and, if they do, find their point of intersection.​

• To understand what is meant when we say that 2 lines are ‘skew’.​

• To be able to prove whether or not 2 lines are skew.

​

• To be able to solve simple vector problems involving scalar product and other simple vector properties.

(66 Slides)​

---

F46. Further Vectors 3
​NEW

• To be able to find the Equation of a Plane in Scalar Product form.

​

• To be able to find the Equation of a Plane in Cartesian form.

• To be able to find the Equation of a Plane in Parametric form.

• To be able to find the Perpendicular Distance from a Point to a Plane.

(51 Slides)​

F47. Further Vectors 4
​NEW

• To be able to find the angle between a line and a plane

​

• To be able to find the angle between 2 planes.

• To be able to find the equation of the line of intersection of 2 planes.

(55 Slides)​

F48. Matrix Solution of Simultaneous Equations 2
​NEW

• To be able to interpret geometrically the solution (and failure of solution) of 3 simultaneous linear equations:

​

• Students should be able to interpret, on analysis of the 3 equations, whether the 3 planes

• meet in a point
• meet in a line (forming a sheaf)
• form a prism
• are all parallel
• are such that 2 of the 3 planes are parallel.
​

• Students should be familiar with the terms ‘dependent‘, ‘consistent’ and ‘inconsistent’.​

(50 Slides)​

---

F49. Volumes of Revolution
​NEW

• To be able to derive the formulae for volumes of revolution about the coordinates axes

• To be able to calculate volumes of revolution about the coordinates axes.

​

• To be able to calculate more complicated volumes of revolution about the coordinates axes.

(69 Slides)​

F50. Mean Value Theorem
​NEW

• To understand and use the Mean Value Theorem for integration.

• To understand the term ‘Root Mean Square Value’ and know how to calculate it for certain functions.

(37 Slides)​

F51. Partial Fractions and Integration
​NEW

• To recall previously encountered partial fractions methods

 (i.e. linear denominators and repeated linear denominators)

• To be able to find partial fractions when there is a quadratic    term in the denominator.

​

• To be able to integrate expression using partial fractions. 

(47 Slides)
​

---

F52. A Geometric View of Determinants
​NEW

• To be able to consider determinants of 2x2 matrices and 3x3 matrices geometrically.

(30 Slides)

F53. Matrix Transformations in 3D
​NEW

• To be able to carry out reflections about one of the coordinate axes in 3 dimensions.

• To be able to carry out rotations about one of the coordinate axes in 3 dimensions.​​

(40 Slides)

F54. Further Vectors 5
​NEW

• To be able to find the distance between 2 parallel lines.

• To be able to find the distance between 2 skew lines.​

(33 Slides)

---

F55. Further Vectors 6
​NEW

• To be able to find the vector product of two vectors.

• To understand various properties of the vector product.

 

• To be able to use the vector product to find perpendicular vectors.

 

• To be able to find certain areas and volumes using the vector product.

(52 Slides)

F56. Further Vectors 7
​NEW

• To be able to find the equation of a line using the vector product.

• To be able to the distance between a point and a line using the vector product.

• To be able to find the shortest distance between two skew lines using the vector product.

 

• To be able to use the vector product to deduce whether or not two lines intersect.

 

• To be able to interpret the vector product geometrically.

(36 Slides)

F57. DeMoivre's Theorem and Application 3
​NEW

• To be able to sum certain series using DeMoivre’s Theorem.

(39 Slides)

---

F58. DeMoivre's Theorem and Applications 4
​NEW

• To be able to solve geometric problems using DeMoivre’s Theorem.

(57 Slides)

F59. Modelling with 1st Order Differential Equations
​NEW

• To be able to model certain situations using 1st order differential equations.

• To be able to model certain situations using coupled 1st order differential equations.

(64 Slides)

F60. Modelling with 2nd Order Differential Equations
​NEW

• To be able to model simple harmonic motion using 2nd order differential equations.

• To be able to model damped (and forced) oscillations using 2nd order differential equations.

(38 Slides)

---

F61. Reduction Formulae
​NEW

• To be able to derive and use reduction formulae for integration.

(47 Slides)

F62. Factorising Determinants
​NEW

• To know and use the basic rules for simplifying determinants.

​

• To be able to factorise determinants.

(57 Slides)

F63. Further Numerical Integration
​NEW

• To be able to approximate the area under a curve using the Mid-Ordinate Rule.

• To be able to approximate the area under a curve using Simpson’s Rule.

(51 Slides)

---

F64. Inequalities Involving Cubic and Quartic Polynomials
​NEW

• To be able to apply the Rational Root Theorem to identify factors of polynomials.

• To be able to use Descartes’ Rule of Signs to identify the nature (signs) of roots of polynomials.

 

• To be able to solve inequalities involving cubic and quartic functions.

(41 Slides)

F65. Modulus of Functions and Associated Inequalities
​NEW

• To be able to recall and use the transformation rules involving the modulus function.

• To be able to solve various types inequalities involving the modulus function.

(57 Slides)

F66. L’Hôpital’s Rule
​NEW

• To be able to use L’Hôpital’s Rule to evaluate certain limits of indeterminate form.

(36 Slides)

---

F67 Length of a Curve
(Formerly F35)

• To find the length of a curve when the curve is given in Cartesian form.

​

•  To find the length of a curve when the curve is given in Parametric form.
  

(20 Slides)
​

F68 Area of Surface of Revolution
(Formerly F41)

• To find the area of surface of revolution for curves given in Cartesian form.

​

•  To find the area of surface of revolution for curves given in Parametric form.
  

(22 Slides)

---

​​A-Level Mathematics PowerPoint Presentations​

These presentations were previously on the A-Level further mathematics syllabus, but have now been moved to the new A-Level mathematics specification.
​

P1 Calculus
(Formerly F2)

P2 Linear Laws
(Formerly F6)

P3 Linear Laws and Logarithms
(Formerly F11)

·         To be able to find the gradient of a curve at any point from first principles.​

(31 Slides)

    To be able to reduce various relations to linear laws.

(41 Slides)
​

·         To recall the laws of logarithms.

·         To be able to use logarithms to reduce certain relations to linear laws.

(25 Slides)

---

 P4 Exact Values of Trigonometric Ratios
(Formerly F17)

P5 Trigonometry (General Solutions)
(Formerly F22)

To be able to deduce trig. ratios of 30, 45 and 60 degrees respectively.

·         To know the relationships sin θ = cos (90-θ) and cos θ = sin(90-θ).

·         To be able to write trig. ratios as trig. ratios of acute angles.

·         To understand what is meant by ‘odd functions’ and ‘even functions’.

(39 Slides)

  To be able to find the general solution of simple trigonometric equations in degrees.

·         To be able to find the general solution of simple trigonometric equations in radians.

(34 Slides)
​

---

Topics included in Packages:
​

Package 1

F1. Asymptotes and Some Rational Functions 1
F2. Complex Numbers 1.
F3. 1st Order Differential Equations.
F4. Improper Integrals 1.
F5. Matrices.
F6. Inequalities involving Rational Expressions
F7. Polar Coordinates 1
F8. Roots of Quadratics
F9. Matrix Transformations.
F10. Asymptotes and Rational Functions 2.
F11. Polar Coordinates 2.
F12. 2nd Order Differential Equations.
​​

Package 2

F13. Complex Numbers 2.
F14. Improper Integrals 2.
F15. Roots of Polynomials
F16.Graphical Solution of Inequalities.
F17. Composite Geometric Transformations using Matrices.
F18. Numerical Methods.
F19. Hyperbolic Functions.
F20. Inverse Trigonometric Functions.
F21. More 1st and 2nd Order Differential Equations 1.
F22. Polar Coordinates 3.
F23. Complex Roots of Polynomials with Real Coefficients.
F24. Series

Package 3

F25. Matrices and Linear Transformations.
F26. DeMoivre's Theorem 1.
F27. Differentiation of Hyperbolic Functions.
F28. Exponential Form of a Complex Number.
F29. Inverse Matrices and Determinants.
F30. Matrix Solution of Simultaneous Equations.
F31. MacLaurin's Series.
F32. Parabolas, Ellipses and Hyperbolas.
F33. The Method of Differences.
F34. Loci in the Complex Plane.
F35. DeMoivre's Theorem 2.
F36. Integration with Hyperbolic Functions 

Package 4

F37. Limits of MacLaurin's Series.
F38. More 1st and 2nd Order Differential Equations 2.
F39. Numerical Methods for 1st Order Differential Equations.
F40. Proof by Mathematical Induction.
F41. Solving Hyperbolic Equations.
F42. Eigenvalues and Eigenvectors.
F43. Diagonalisation of a Matrix.
F44. Further Vectors 1
F45. Further Vectors 2
F46. Further Vectors 3
F47. Further Vectors 4
​F48. Matrix Solution of Simultaneous Equations 2

Package 5

F49. Volumes of Revolution
F50. Mean Value Theorem
F51. Partial Fractions and Integration
F52. A Geometric View of Determinants
F53. Matrix Transformations in 3D
F54. Further Vectors 5
F55. Further Vectors 6
F56. Further Vectors 7
F57. DeMoivre's Theorem 3
F58. DeMoivre's Theorem 4
F59. Modelling with 1st Order Differential Equations
F60. Modelling with 2nd Order Differential Equations
F61. Reduction Formulae
F62. Factorising Determinants
F63. Further Numerical Integration
F64. Inequalities Involving Cubic and Quartic Polynomials
F65. Modulus of Functions and Associated Inequalities.
F66. L'Hôpital's Rule
F67 Length of a Curve
​F68 Area of Surface of Revolution

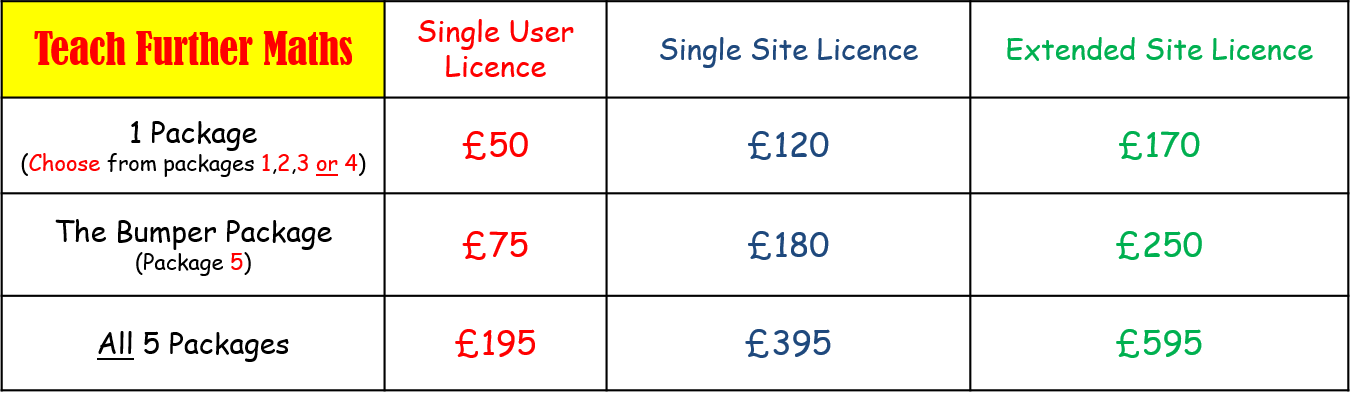
Value Package Prices:

​There are 4 standard packages containing 12 presentations per package (see above).

There is also now a bumper 5th package, containing the remaining 20 presentations that complete the

compulsory core teaching content
​
for all of the main examination boards (AQA, Edexcel, OCR and MEI).
​

​
​Licence Types:

​
​Single User Licence: For use on one single computer at one location. Suitable for student home use or private tutoring.
(NOTE: A SINGLE USER LICENCE IS NOT SUITABLE FOR SCHOOL USE. )

Single Site Licence: For use on multiple computers at one location. Suitable for school use.
(NOTE: USE BY ONE TEACHER AT ONE SCHOOL STILL REQUIRES A SITE LICENCE)

Extended Site Licence: Same as single site licence but also includes use at home by staff/students and VLE use.
​

Purchase Single Package (Package 1,2,3 or 4)

​Send an email to 
SmartProducts@talktalk.net 
stating the number of the package required, as well as the licence type needed.

You will received a confirmatory response (usually within 1 working day), containing the necessary bank details for your payment. 

Purchase Bumper Package
(Package 5)

​Send an email to 
SmartProducts@talktalk.net 
stating the number of the package required, as well as the licence type needed.

You will received a confirmatory response (usually within 1 working day), containing the necessary bank details for your payment. 
​

Purchase All 5 Packages​

​​Send an email to 
SmartProducts@talktalk.net 
stating that you require ALL packages.
 Please also state the licence type needed.

You will received a confirmatory response (usually within 1 working day), containing the necessary bank details for your payment. 

---

​
​​NOTE:  ISSUES FOR CUSTOMERS WITH PAYPAL PAYMENTS
​

SEVERAL CUSTOMERS HAVE RECENTLY INFORMED US THAT THEY HAVE BEEN HAVING DIFFICULTIES MAKING THEIR PURCHASE VIA PAYPAL.

WE HAVE THEREFORE TEMPORARILY REMOVED THE OPTION TO PAY VIA PAYPAL UNTIL THE MATTER CAN BE RESOLVED.

INSTEAD, WE NOW ASK THAT ANY PAYMENTS ARE MADE VIA DIRECT (BACS) BANK TRANSFER (EMAIL US FOR DETAILS - SEE ABOVE)

---

NOTE: Purchase Orders are welcome.
Email SmartProducts@talktalk.net with your purchase order number and we send you an invoice along with acceptable methods of payment.
​
Payment by BACS transfer is also welcome.
Email SmartProducts@talktalk.net to request the relevant bank details.

​
​

​Individual Presentations

If you only wish to purchase individual presentations, then you may still do so at the prices stated below.

Simply let us know the name and number of your desired presentations when you order.
​
Individual PowerPoint presentations will be uploaded to an email address of your choosing, once payment has been made.
(PLEASE ALLOW 1 WORKING DAY FOR YOUR PRESENTATION(S) TO BE UPLOADED TO YOU)

​Send the correct amount (see table above) from your PayPal account to SmartProducts@talktalk.net along with the name and/or number of the presentation required.
​

​Note: Your presentations will be be sent to you via email, usually within one working day from payment being received.

Purchases made will be non-refundable (although excellent customer service will be provided to ensure that you are entirely satisfied with the product).

Please do view the FAQs page for important information about using the presentations.

If you have any other queries/questions, then please do ask (see contact page).

We will always be happy to help and assist you in any way we can.

Enjoy 'Teach Further Maths'!

Tweet

Follow @TeachFMaths

Teach Further Maths by P. A. Hunt

Large Visitor Globe